Hyperparameter Range of Value
Motivation
Tuning/Optimizing the hyperparameters during training can significantly reduce training time and increase training accuracy. I will not be listing the hyperparameters for tuning, just methods. I assume you have an understanding of how to analyze whether your model is exhibiting high variance or high bias which will be an important part of the feedback loop to optimizing the cost function.
During this process, we are interested in how well the model performs after a certain number of epochs/iterations through our dataset. The numbers picked for this are generally up to you and should take into account computational resources as well as accuracy requirements.
Choosing Parameter Space
For each parameter, we’ll need to decide a range of values. It’s tempting to always pick randomly from a linear scale but we’ll see that’s not always the case. It’s important to pick the appropriate scale for the random distribution. Sometimes it can be easier to think of it in terms of “what values do I want to make sure I check” and then pick the appropriate parameter space.
Linear Space
Use this when we want to distribute the values over the linear space. As an example, let’s say we want to search from 0.0001-1. With a linear space distribution, 10% of your values would come from 0-0.1 and 90% of your values come from 0.1-1. This is most often used for choosing the number of layers or the number of hidden units \( n^{[l]} \)
Log Space
We can use this when we want to distribute the values over the logarithmic space. In the same example above, let’s say we want to search from 0.0001-1. Instead of having only 10% of the values come from 0.0001-0.1, we would see the values distributed evenly across each order of magnitude; 0.0001-0.001, 0.001-0.01, 0.01-0.1, 0.1-1, would all have the same distribution of values we could pick from. In situations where we pick parameters for exponentially weighted averages, this can be important to evenly explore all orders of magnitude.
\( r \in [-4, 0] \) for learning rate \( \alpha \in [10^{-4}, 1] \)
r = -4 * np.random.rand()
learning_rate = 10**r
\( r \in [-3, -1] \) an example for exponentially weighted averages where you want \( 1-\beta \in [10^{-1}, 10^{-3}]\)
r = -3 * np.random.rand()
beta = 1 - 10**r
Checking Parameters
Let’s quickly discuss some common ways to generate the values for the parameters we pick. I’ll include some that may seem like a good idea, but would not be optimal for most use cases.
Ordered
It’s tempting to iterate through each hyperparameter “set” in order; increment hp1 from it’s min to max while holding hp2 constant and then increment hp2. This ends up being relatively inefficient and should be avoided.
Randomly
Although generally agreed to be better than the systematic method listed above, there isn’t a good way to find our optimal set. There are significantly better ways that are relatively simple.
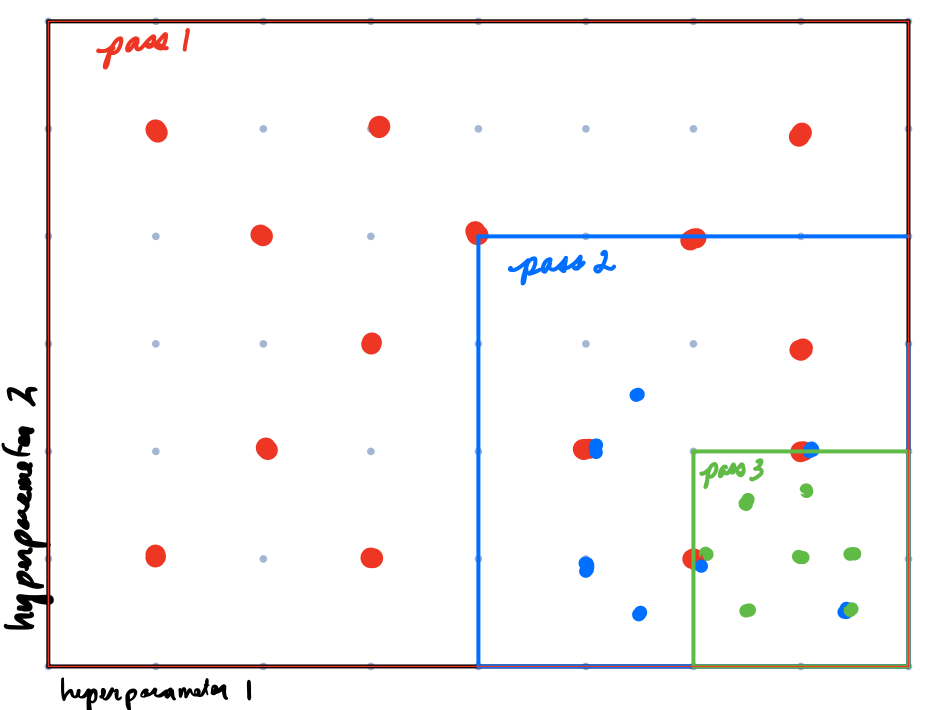
Course to Fine
Conceptually, this can be thought of as a combination of the previous two “methods”. Begin by randomly picking evenly across the range of values we want to explore. See which section gave us optimal parameters and “zoom into” the section. Repeat until we find a set of values that meet your criteria as described above.