Classification Model Performance Metrics
Intro
Using the additional below metrics, in addition to the typical error/accuracy, can help when optimizing the model hyperparameters. This is particularly true when working with skewed classes. There are also product-specific use cases to optimize one set of the below parameters over another. For example, if a user story requires that nothing is missed and is willing to have some false positives, then recall is important. Conversely, if a user wants to only make sure that positive predictors are extremely accurate, then precision is important
From a product development perspective, it is important to understand these metrics ahead of time before model training so that the correct hyperparameters can be picked.
Confusion Matrix
| Hypothesis class | |||
| 1 | 0 | ||
| Ground-truth class | 1 | True Positives | False Negatives Type II error |
| 0 | False Positives Type I error |
True Negatives | |
Metrics
Accuracy
Accurate predictions occur when their average is near the quantity being measured. In the context of classification, it identifies how well the model identified or excluded a condition. \[ ACC = \frac{TP + TN}{P + N} = \frac{TP + TN}{TP + TN + FP + FN} \]
Precision
Aka: positive predictive value (PPV) is the fraction of the results that are relevant to the query. Superfluous results go against this score, but missed results do not. \[ PPV = \frac{TP}{TP + FP} = 1 - FDR \]
Recall / Sensitivity
Aka: sensitivity, hit rate, true positive rate (TPR) is the fraction of the results that are successfully retrieved. Missed results go against this core, but superfluous results do not. \[ TPR = \frac{TP}{TP+FN} = 1 - FNR \]
Specificity
Aka: selectivity, true negative rate (TNR) \[ TNR = \frac{TN}{TN + FP} = 1 - FPR \]
1-Specificity
Aka: False positive rate (FPR)
F1 Score
A hybrid metric that is useful when there are unbalanced classes and the same importance is given to precision and recall. \[ F_1 = 2 \cdot \frac{PPV \cdot TPR}{PPV + TPR} \]
F𝜷 Score
More generalized F1 Score where a 𝜷 > 1 emphasizes recall over than precision and a 𝜷 < 1 weights precision as being more important than recall \[ F_\beta = (1 + \beta^2) \cdot \frac{PPV \cdot TPR}{\beta^2 \cdot PPV + TPR} \]
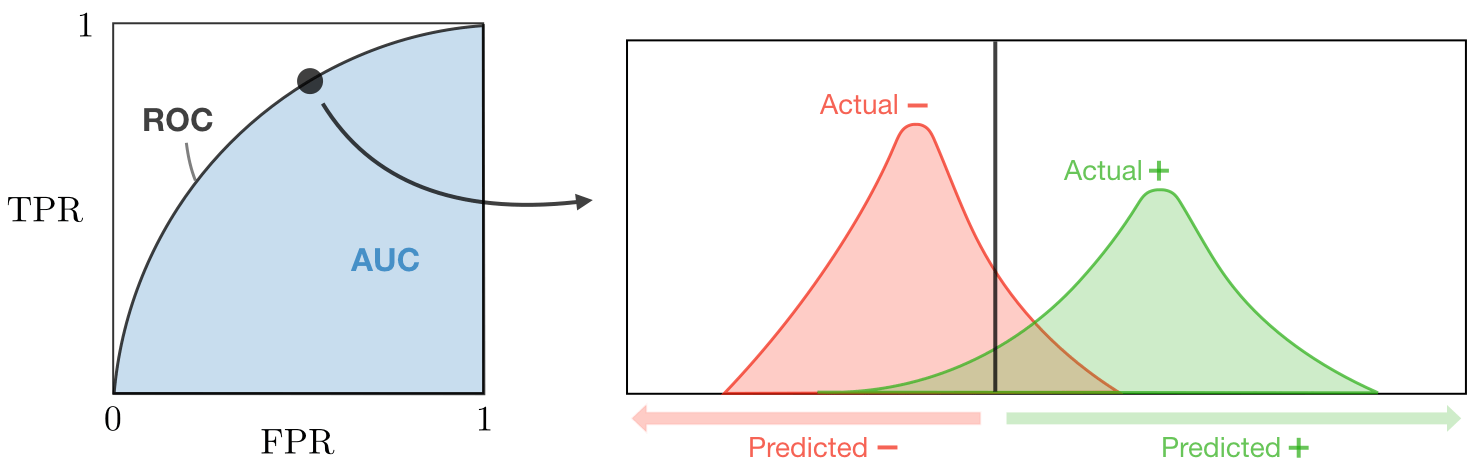
ROC / AUC
The receiver operating curve is the plot of TPR vs FPR with AUC being the area under the ROC aka AUC/AUROC. This describes how well the model is capable of distinguishing between classes.